H.265/HEVC(High Efficiency Video Coding)のリファレンスソフトウェア(HM)のTComRdCost::xGetHADs関数について学んでいきます。
TComRdCost::xGetHADs()
Distortion TComRdCost::xGetHADs( DistParam* pcDtParam )
{
if ( pcDtParam->bApplyWeight )
{
return TComRdCostWeightPrediction::xGetHADsw( pcDtParam );
}
const Pel* piOrg = pcDtParam->pOrg;
const Pel* piCur = pcDtParam->pCur;
const Int iRows = pcDtParam->iRows;
const Int iCols = pcDtParam->iCols;
const Int iStrideCur = pcDtParam->iStrideCur;
const Int iStrideOrg = pcDtParam->iStrideOrg;
const Int iStep = pcDtParam->iStep;
Int x, y;
Distortion uiSum = 0;
if( ( iRows % 8 == 0) && (iCols % 8 == 0) )
{
Int iOffsetOrg = iStrideOrg<<3;
Int iOffsetCur = iStrideCur<<3;
for ( y=0; y<iRows; y+= 8 )
{
for ( x=0; x<iCols; x+= 8 )
{
uiSum += xCalcHADs8x8( &piOrg[x], &piCur[x*iStep], iStrideOrg, iStrideCur, iStep
#if VECTOR_CODING__DISTORTION_CALCULATIONS && (RExt__HIGH_BIT_DEPTH_SUPPORT==0)
, pcDtParam->bitDepth
#endif
);
}
piOrg += iOffsetOrg;
piCur += iOffsetCur;
}
}
else if( ( iRows % 4 == 0) && (iCols % 4 == 0) )
{
Int iOffsetOrg = iStrideOrg<<2;
Int iOffsetCur = iStrideCur<<2;
for ( y=0; y<iRows; y+= 4 )
{
for ( x=0; x<iCols; x+= 4 )
{
uiSum += xCalcHADs4x4( &piOrg[x], &piCur[x*iStep], iStrideOrg, iStrideCur, iStep );
}
piOrg += iOffsetOrg;
piCur += iOffsetCur;
}
}
else if( ( iRows % 2 == 0) && (iCols % 2 == 0) )
{
Int iOffsetOrg = iStrideOrg<<1;
Int iOffsetCur = iStrideCur<<1;
for ( y=0; y<iRows; y+=2 )
{
for ( x=0; x<iCols; x+=2 )
{
uiSum += xCalcHADs2x2( &piOrg[x], &piCur[x*iStep], iStrideOrg, iStrideCur, iStep );
}
piOrg += iOffsetOrg;
piCur += iOffsetCur;
}
}
else
{
assert(false);
}
return ( uiSum >> DISTORTION_PRECISION_ADJUSTMENT(pcDtParam->bitDepth-8) );
}xGetHADs()はブロックサイズが8x8以上であればxCalcHADs8x8()を実行、4x4であればxCalcHADs4x4()を実行、2x2であればxCalcHADs2x2()を実行します。xCalcHADsNxN()はNxNのブロック毎に残差ブロックに対してアダマール変換を実行し、変換後の係数からSATD(Sum of Absolute Transformed Differences)を算出します。
アダマール変換は値が+1または-1のいずれかを取る矩形波を基底関数とする直交変換のことです。HEVCでは8x8や4x4の残差ブロックにアダマール行列(狭義ではウォルシュ行列とも呼ばれるそうです)を前後から2回掛けることで、簡易な周波数変換として用いられています。
TComRdCost::xCalcHADs2x2()
Distortion TComRdCost::xCalcHADs2x2( const Pel *piOrg, const Pel *piCur, Int iStrideOrg, Int iStrideCur, Int iStep )
{
Distortion satd = 0;
TCoeff diff[4], m[4];
assert( iStep == 1 );
diff[0] = piOrg[0 ] - piCur[0];
diff[1] = piOrg[1 ] - piCur[1];
diff[2] = piOrg[iStrideOrg ] - piCur[0 + iStrideCur];
diff[3] = piOrg[iStrideOrg + 1] - piCur[1 + iStrideCur];
m[0] = diff[0] + diff[2];
m[1] = diff[1] + diff[3];
m[2] = diff[0] - diff[2];
m[3] = diff[1] - diff[3];
satd += abs(m[0] + m[1]);
satd += abs(m[0] - m[1]);
satd += abs(m[2] + m[3]);
satd += abs(m[2] - m[3]);
return satd;
}xCalcHADs2x2()では最初に2x2の残差ブロックを生成し、残差ブロックに対してアダマール行列を前後から2回掛けることで周波数変換を行い、最後に変換係数の総和を算出しています。
ここで、アダマール変換に用いる2x2の行列の例を以下に示します。
\[ H = \left( \begin{array}{rr} 1 & 1 \\ 1 & -1 \end{array} \right) \]
ここで、2x2の残差ブロックを \( X = \left( \begin{array}{cc} d_0 & d_1 \\ d_2 & d_3 \end{array} \right) \) と書くと、xCalcHADs2x2()で実行されるアダマール変換は以下の式となります。
\[ HXH^T = \left( \begin{array}{rr} 1 & 1 \\ 1 & -1 \end{array} \right) \left( \begin{array}{cc} d_0 & d_1 \\ d_2 & d_3 \end{array} \right) \left( \begin{array}{rr} 1 & 1 \\ 1 & -1 \end{array} \right) \]
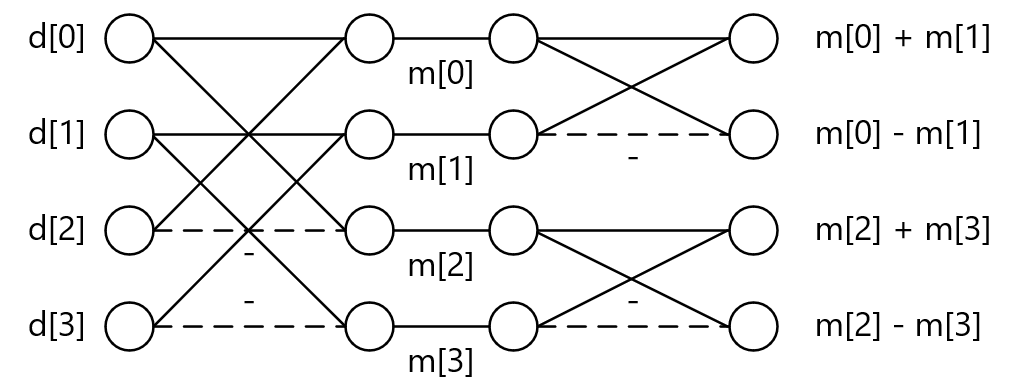
コードの中では、最初に\(H\)と\(X\)の積を計算し、次に\(HX\)と\(H^T\)の積を計算します。この演算は以下のようにバタフライ演算でも表現することができます。コード中の配列mは、バタフライ演算の途中経路の値です。
\[ HXH^T = \left( \begin{array}{rr} 1 & 1 \\ 1 & -1 \end{array} \right) \left( \begin{array}{cc} d_0 & d_1 \\ d_2 & d_3 \end{array} \right) \left( \begin{array}{rr} 1 & 1 \\ 1 & -1 \end{array} \right) = \left( \begin{array}{cc} m_0 & m_1 \\ m_2 & m_3 \end{array} \right) \left( \begin{array}{rr} 1 & 1 \\ 1 & -1 \end{array} \right) = \left( \begin{array}{cc} m_0+m_1 & m_0-m_1 \\ m_2+m_3 & m_2-m_3 \end{array} \right) \]
TComRdCost::xCalcHADs4x4()
Distortion TComRdCost::xCalcHADs4x4( const Pel *piOrg, const Pel *piCur, Int iStrideOrg, Int iStrideCur, Int iStep )
{
Int k;
Distortion satd = 0;
TCoeff diff[16], m[16], d[16];
assert( iStep == 1 );
// 残差行列を生成する
for( k = 0; k < 16; k+=4 )
{
diff[k+0] = piOrg[0] - piCur[0];
diff[k+1] = piOrg[1] - piCur[1];
diff[k+2] = piOrg[2] - piCur[2];
diff[k+3] = piOrg[3] - piCur[3];
piCur += iStrideCur;
piOrg += iStrideOrg;
}
/*===== hadamard transform =====*/
// 1回目のアダマール変換
m[ 0] = diff[ 0] + diff[12];
m[ 1] = diff[ 1] + diff[13];
m[ 2] = diff[ 2] + diff[14];
m[ 3] = diff[ 3] + diff[15];
m[ 4] = diff[ 4] + diff[ 8];
m[ 5] = diff[ 5] + diff[ 9];
m[ 6] = diff[ 6] + diff[10];
m[ 7] = diff[ 7] + diff[11];
m[ 8] = diff[ 4] - diff[ 8];
m[ 9] = diff[ 5] - diff[ 9];
m[10] = diff[ 6] - diff[10];
m[11] = diff[ 7] - diff[11];
m[12] = diff[ 0] - diff[12];
m[13] = diff[ 1] - diff[13];
m[14] = diff[ 2] - diff[14];
m[15] = diff[ 3] - diff[15];
d[ 0] = m[ 0] + m[ 4];
d[ 1] = m[ 1] + m[ 5];
d[ 2] = m[ 2] + m[ 6];
d[ 3] = m[ 3] + m[ 7];
d[ 4] = m[ 8] + m[12];
d[ 5] = m[ 9] + m[13];
d[ 6] = m[10] + m[14];
d[ 7] = m[11] + m[15];
d[ 8] = m[ 0] - m[ 4];
d[ 9] = m[ 1] - m[ 5];
d[10] = m[ 2] - m[ 6];
d[11] = m[ 3] - m[ 7];
d[12] = m[12] - m[ 8];
d[13] = m[13] - m[ 9];
d[14] = m[14] - m[10];
d[15] = m[15] - m[11];
// 2回目のアダマール変換
m[ 0] = d[ 0] + d[ 3];
m[ 1] = d[ 1] + d[ 2];
m[ 2] = d[ 1] - d[ 2];
m[ 3] = d[ 0] - d[ 3];
m[ 4] = d[ 4] + d[ 7];
m[ 5] = d[ 5] + d[ 6];
m[ 6] = d[ 5] - d[ 6];
m[ 7] = d[ 4] - d[ 7];
m[ 8] = d[ 8] + d[11];
m[ 9] = d[ 9] + d[10];
m[10] = d[ 9] - d[10];
m[11] = d[ 8] - d[11];
m[12] = d[12] + d[15];
m[13] = d[13] + d[14];
m[14] = d[13] - d[14];
m[15] = d[12] - d[15];
d[ 0] = m[ 0] + m[ 1];
d[ 1] = m[ 0] - m[ 1];
d[ 2] = m[ 2] + m[ 3];
d[ 3] = m[ 3] - m[ 2];
d[ 4] = m[ 4] + m[ 5];
d[ 5] = m[ 4] - m[ 5];
d[ 6] = m[ 6] + m[ 7];
d[ 7] = m[ 7] - m[ 6];
d[ 8] = m[ 8] + m[ 9];
d[ 9] = m[ 8] - m[ 9];
d[10] = m[10] + m[11];
d[11] = m[11] - m[10];
d[12] = m[12] + m[13];
d[13] = m[12] - m[13];
d[14] = m[14] + m[15];
d[15] = m[15] - m[14];
// 変換係数の総和を算出
for (k=0; k<16; ++k)
{
satd += abs(d[k]);
}
satd = ((satd+1)>>1);
return satd;
}xCalcHADs4x4()も処理の流れは2x2と同様です。残差ブロックに対してアダマール行列を前後から2回掛けることで周波数変換を行い、最後に変換係数の総和を算出しています。
ここで、アダマール変換に用いる4x4の行列の例を以下に示します。
\[ H = \left( \begin{array}{rrrr} 1 & 1 & 1 & 1 \\ 1 & -1 & 1 & -1 \\ 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 \end{array} \right) \]
xCalcHADs4x4()では上の行列をそのまま利用せず、各行ごとの符号反転の回数(周波数)が昇順になるように行を並び替えています。以下の行列では、上の行から順に符号反転の回数が0, 1, 2, 3と変化していることがわかります。
\[ H = \left( \begin{array}{rrrr} 1 & 1 & 1 & 1 \\ 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 \\ 1 & -1 & 1 & -1 \end{array} \right) \]
ウォルシュ行列の行の並び替えについてはWikipediaにも記載があります。
ここで、4x4の残差ブロックを \( X = \left( \begin{array}{cccc} d_0 & d_1 & d_2 & d_3 \\ d_4 & d_5 & d_6 & d_7 \\ d_8 & d_9 & d_{10} & d_{11} \\ d_{12} & d_{13} & d_{14} & d_{15} \end{array} \right) \) と書くと、xCalcHADs4x4()で実行されるアダマール変換は以下の式となります。
\[ HXH^T = \left( \begin{array}{rrrr} 1 & 1 & 1 & 1 \\ 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 \\ 1 & -1 & 1 & -1 \end{array} \right) \left( \begin{array}{cccc} d_0 & d_1 & d_2 & d_3 \\ d_4 & d_5 & d_6 & d_7 \\ d_8 & d_9 & d_{10} & d_{11} \\ d_{12} & d_{13} & d_{14} & d_{15} \end{array} \right) \left( \begin{array}{rrrr} 1 & 1 & 1 & 1 \\ 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 \\ 1 & -1 & 1 & -1 \end{array} \right) \]
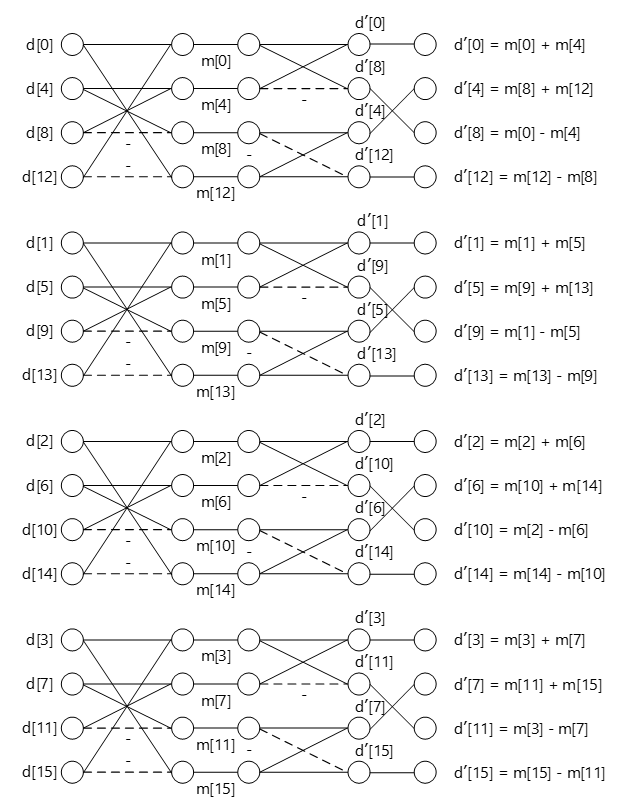
コードの中では、最初に\(H\)と\(X\)の積を計算し、次に\(HX\)と\(H^T\)の積を計算します。まず、\(H\)と\(X\)の積の演算のみに着目すると、この演算は以下のようにバタフライ演算でも表現することができます。コード中の配列mは、このバタフライ演算の途中経路の値です。
バタフライ演算形式で見ると、残差ブロックの各列ごとに全く同じ演算を実行しているため、並列計算可能であることがわかります。また、演算の最後に行列の2行目と3行目を入れ替えていることもわかります。
\[ HX = \left( \begin{array}{rrrr} 1 & 1 & 1 & 1 \\ 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 \\ 1 & -1 & 1 & -1 \end{array} \right) \left( \begin{array}{cccc} d_0 & d_1 & d_2 & d_3 \\ d_4 & d_5 & d_6 & d_7 \\ d_8 & d_9 & d_{10} & d_{11} \\ d_{12} & d_{13} & d_{14} & d_{15} \end{array} \right) = \left( \begin{array}{cccc} m_0+m_4 & m_1+m_5 & m_2+m_6 & m_3+m_7 \\ m_8+m_{12} & m_9+m_{13} & m_{10}+m_{14} & m_{11}+m_{15} \\ m_0-m_4 & m_1-m_5 & m_2-m_6 & m_3-m_7 \\ m_{12}-m_8 & m_{13}-m_9 & m_{14}-m_{10} & m_{15}-m_{11} \end{array} \right) = \left( \begin{array}{cccc} d'_0 & d'_1 & d'_2 & d'_3 \\ d'_4 & d'_5 & d'_6 & d'_7 \\ d'_8 & d'_9 & d'_{10} & d'_{11} \\ d'_{12} & d'_{13} & d'_{14} & d'_{15} \end{array} \right) \]
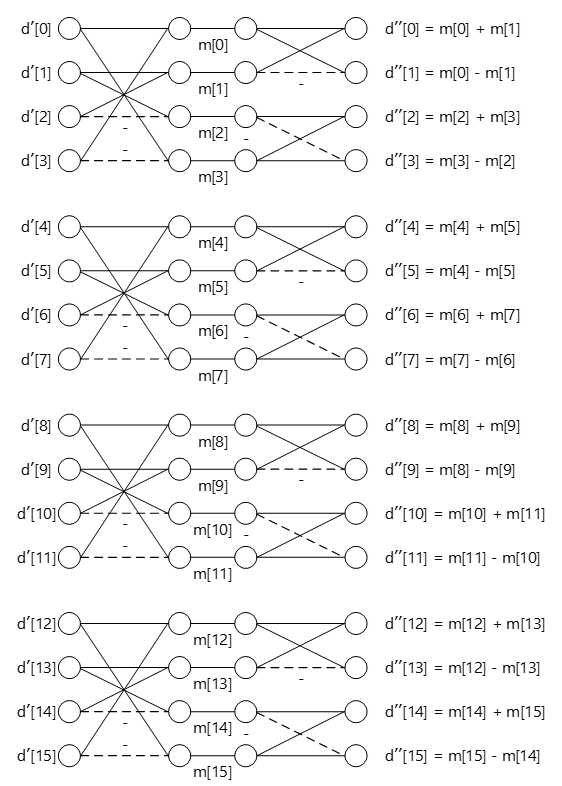
\(HX\)と\(H^T\)の積も同様にバタフライ演算で表現可能です。
\(HX\)の演算結果に対して各行ごとに全く同じ演算を実行しています。演算により得られた行列の2列目と3列目の要素の添字の順番が入れ替わっていますが(バタフライ演算過程で列の入れ替えを行っていないため)、SATDを算出する(変換係数の総和をとる)だけなので特に問題は生じません。
\[ (HX)H^T= \left( \begin{array}{cccc} d'_0 & d'_1 & d'_2 & d'_3 \\ d'_4 & d'_5 & d'_6 & d'_7 \\ d'_8 & d'_9 & d'_{10} & d'_{11} \\ d'_{12} & d'_{13} & d'_{14} & d'_{15} \end{array} \right) \left( \begin{array}{rrrr} 1 & 1 & 1 & 1 \\ 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 \\ 1 & -1 & 1 & -1 \end{array} \right) = \left( \begin{array}{cccc} m'_0+m'_1 & m'_0-m'_1 & m'_2+m'_3 & m'_3-m'_2 \\ m'_4+m'_5 & m'_4-m'_5 & m'_6+m'_7 & m'_7-m'_6 \\ m'_8+m'_9 & m'_8-m'_9 & m'_{10}+m'_{11} & m'_{11}-m'_{10} \\ m'_{12}+m'_{13} & m'_{12}-m'_{13} & m'_{14}+m'_{15} & m'_{15}-m'_{14} \end{array} \right) = \left( \begin{array}{cccc} d^{''}_0 & d^{''}_2 & d^{''}_1 & d^{''}_3 \\ d^{''}_4 & d^{''}_6 & d^{''}_5 & d^{''}_7 \\ d^{''}_8 & d^{''}_{10} & d^{''}_{9} & d^{''}_{11} \\ d^{''}_{12} & d^{''}_{14} & d^{''}_{13} & d^{''}_{15} \end{array} \right) \]
TComRdCost::xCalcHADs8x8()
Distortion TComRdCost::xCalcHADs8x8( const Pel *piOrg, const Pel *piCur, Int iStrideOrg, Int iStrideCur, Int iStep
#if VECTOR_CODING__DISTORTION_CALCULATIONS && (RExt__HIGH_BIT_DEPTH_SUPPORT==0)
, Int bitDepth
#endif
)
{
// SIMD演算が可能な場合はsimdHADs8x8()を実行して終了する
#if VECTOR_CODING__DISTORTION_CALCULATIONS && (RExt__HIGH_BIT_DEPTH_SUPPORT==0)
if( bitDepth <= 10 )
{
return( simdHADs8x8( piOrg , piCur , iStrideOrg , iStrideCur ) );
}
#endif
Int k, i, j, jj;
Distortion sad = 0;
TCoeff diff[64], m1[8][8], m2[8][8], m3[8][8];
assert( iStep == 1 );
// 残差行列を生成する
for( k = 0; k < 64; k += 8 )
{
diff[k+0] = piOrg[0] - piCur[0];
diff[k+1] = piOrg[1] - piCur[1];
diff[k+2] = piOrg[2] - piCur[2];
diff[k+3] = piOrg[3] - piCur[3];
diff[k+4] = piOrg[4] - piCur[4];
diff[k+5] = piOrg[5] - piCur[5];
diff[k+6] = piOrg[6] - piCur[6];
diff[k+7] = piOrg[7] - piCur[7];
piCur += iStrideCur;
piOrg += iStrideOrg;
}
//horizontal
for (j=0; j < 8; j++)
{
jj = j << 3;
m2[j][0] = diff[jj ] + diff[jj+4];
m2[j][1] = diff[jj+1] + diff[jj+5];
m2[j][2] = diff[jj+2] + diff[jj+6];
m2[j][3] = diff[jj+3] + diff[jj+7];
m2[j][4] = diff[jj ] - diff[jj+4];
m2[j][5] = diff[jj+1] - diff[jj+5];
m2[j][6] = diff[jj+2] - diff[jj+6];
m2[j][7] = diff[jj+3] - diff[jj+7];
m1[j][0] = m2[j][0] + m2[j][2];
m1[j][1] = m2[j][1] + m2[j][3];
m1[j][2] = m2[j][0] - m2[j][2];
m1[j][3] = m2[j][1] - m2[j][3];
m1[j][4] = m2[j][4] + m2[j][6];
m1[j][5] = m2[j][5] + m2[j][7];
m1[j][6] = m2[j][4] - m2[j][6];
m1[j][7] = m2[j][5] - m2[j][7];
m2[j][0] = m1[j][0] + m1[j][1];
m2[j][1] = m1[j][0] - m1[j][1];
m2[j][2] = m1[j][2] + m1[j][3];
m2[j][3] = m1[j][2] - m1[j][3];
m2[j][4] = m1[j][4] + m1[j][5];
m2[j][5] = m1[j][4] - m1[j][5];
m2[j][6] = m1[j][6] + m1[j][7];
m2[j][7] = m1[j][6] - m1[j][7];
}
//vertical
for (i=0; i < 8; i++)
{
m3[0][i] = m2[0][i] + m2[4][i];
m3[1][i] = m2[1][i] + m2[5][i];
m3[2][i] = m2[2][i] + m2[6][i];
m3[3][i] = m2[3][i] + m2[7][i];
m3[4][i] = m2[0][i] - m2[4][i];
m3[5][i] = m2[1][i] - m2[5][i];
m3[6][i] = m2[2][i] - m2[6][i];
m3[7][i] = m2[3][i] - m2[7][i];
m1[0][i] = m3[0][i] + m3[2][i];
m1[1][i] = m3[1][i] + m3[3][i];
m1[2][i] = m3[0][i] - m3[2][i];
m1[3][i] = m3[1][i] - m3[3][i];
m1[4][i] = m3[4][i] + m3[6][i];
m1[5][i] = m3[5][i] + m3[7][i];
m1[6][i] = m3[4][i] - m3[6][i];
m1[7][i] = m3[5][i] - m3[7][i];
m2[0][i] = m1[0][i] + m1[1][i];
m2[1][i] = m1[0][i] - m1[1][i];
m2[2][i] = m1[2][i] + m1[3][i];
m2[3][i] = m1[2][i] - m1[3][i];
m2[4][i] = m1[4][i] + m1[5][i];
m2[5][i] = m1[4][i] - m1[5][i];
m2[6][i] = m1[6][i] + m1[7][i];
m2[7][i] = m1[6][i] - m1[7][i];
}
for (i = 0; i < 8; i++)
{
for (j = 0; j < 8; j++)
{
sad += abs(m2[i][j]);
}
}
sad=((sad+2)>>2);
return sad;
}xCalcHADs8x8()も処理の流れは4x4と同様ですが、行列積の計算順序が異なります。xCalcHADs8x8()では\( X \)と\( H^T \)の積を先に計算し、次に\( H \)と\( XH^T \)の積を計算します。それぞれの行列積は前述のようにバタフライ演算で表現可能です。下図では行列積\( XH^T \)の1行目の結果に対する演算のみに着目してバタフライ演算で表現しています。2行目~8行目も同様の演算が適用されます。
\[ XH^T = \left( \begin{array}{cccc} d_0 & d_1 & d_2 & d_3 & d_4 & d_5 & d_6 & d_7 \\ d_8 & d_9 & d_{10} & d_{11} & d_{12} & d_{13} & d_{14} & d_{15} \\ d_{16} & d_{17} & d_{18} & d_{19} & d_{20} & d_{21} & d_{22} & d_{23} \\ d_{24} & d_{25} & d_{26} & d_{27} & d_{28} & d_{29} & d_{30} & d_{31} \\ d_{32} & d_{33} & d_{34} & d_{35} & d_{36} & d_{37} & d_{38} & d_{39} \\ d_{40} & d_{41} & d_{42} & d_{43} & d_{44} & d_{45} & d_{46} & d_{47} \\ d_{48} & d_{49} & d_{50} & d_{51} & d_{52} & d_{53} & d_{54} & d_{55} \\ d_{56} & d_{57} & d_{58} & d_{59} & d_{60} & d_{61} & d_{62} & d_{63} \end{array} \right) \left( \begin{array}{rrrr} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 \\ 1 & 1 & -1 & -1 & 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 & 1 & -1 & -1 & 1 \\ 1 & 1 & 1 & 1 & -1 & -1 & -1 & -1 \\ 1 & -1 & 1 & -1 & -1 & 1 & -1 & 1 \\ 1 & 1 & -1 & -1 & -1 & -1 & 1 & 1 \\ 1 & -1 & -1 & 1 & -1 & 1 & 1 & -1 \end{array} \right) \]
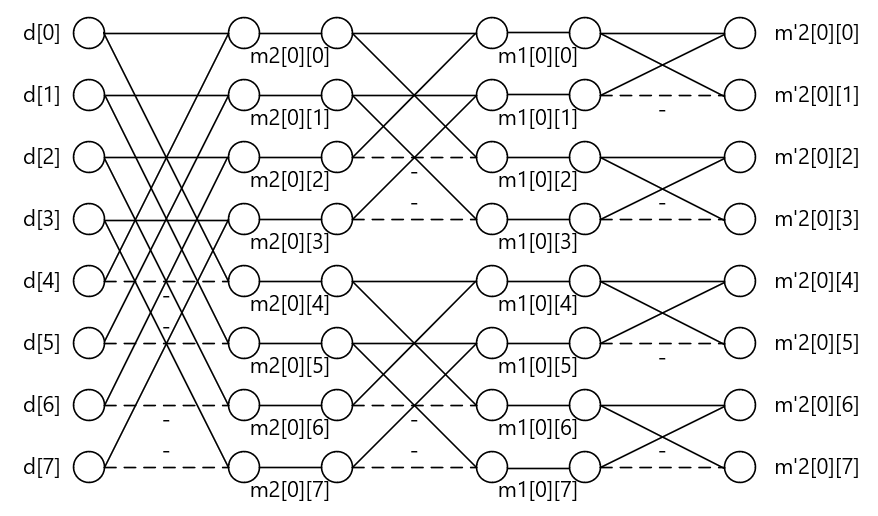
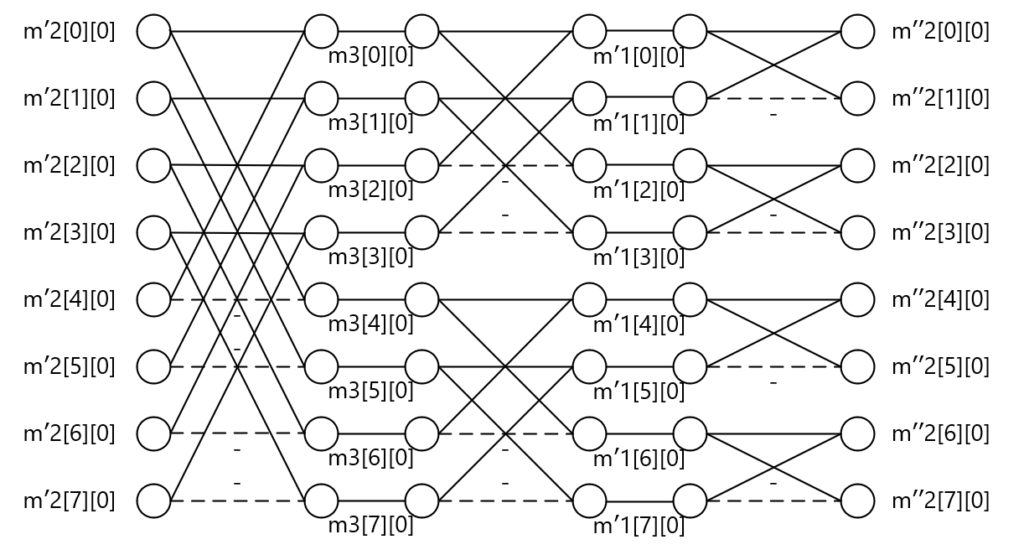
\( H \)と\( XH^T \)の積も同様にバタフライ演算で表現可能です。下図では行列積\( HXH^T \)の1列目の結果に対する演算のみに着目してバタフライ演算で表現しています。2列目~8列目も同様の演算が適用されます。
\[ H(XH^T)= \left( \begin{array}{rrrr} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 \\ 1 & 1 & -1 & -1 & 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 & 1 & -1 & -1 & 1 \\ 1 & 1 & 1 & 1 & -1 & -1 & -1 & -1 \\ 1 & -1 & 1 & -1 & -1 & 1 & -1 & 1 \\ 1 & 1 & -1 & -1 & -1 & -1 & 1 & 1 \\ 1 & -1 & -1 & 1 & -1 & 1 & 1 & -1 \end{array} \right) \left( \begin{array}{rrrr} m'2[0][0] & m'2[0][1] & m'2[0][2] & m'2[0][3] & m'2[0][4] & m'2[0][5] & m'2[0][6] & m'2[0][7] \\ m'2[1][0] & m'2[1][1] & m'2[1][2] & m'2[1][3] & m'2[1][4] & m'2[1][5] & m'2[1][6] & m'2[1][7] \\ m'2[2][0] & m'2[2][1] & m'2[2][2] & m'2[2][3] & m'2[2][4] & m'2[2][5] & m'2[2][6] & m'2[2][7] \\ m'2[3][0] & m'2[3][1] & m'2[3][2] & m'2[3][3] & m'2[3][4] & m'2[3][5] & m'2[3][6] & m'2[3][7] \\ m'2[4][0] & m'2[4][1] & m'2[4][2] & m'2[4][3] & m'2[4][4] & m'2[4][5] & m'2[4][6] & m'2[4][7] \\ m'2[5][0] & m'2[5][1] & m'2[5][2] & m'2[5][3] & m'2[5][4] & m'2[5][5] & m'2[5][6] & m'2[5][7] \\ m'2[6][0] & m'2[6][1] & m'2[6][2] & m'2[6][3] & m'2[6][4] & m'2[6][5] & m'2[6][6] & m'2[6][7] \\ m'2[7][0] & m'2[7][1] & m'2[7][2] & m'2[7][3] & m'2[7][4] & m'2[7][5] & m'2[7][6] & m'2[7][7] \end{array} \right) \]